Geometría Analítica
INTRODUCCIÓN
En los cursos anteriores de matemáticas I y matemáticas II estudiamos el álgebra y la geometría euclidiana; ahora estudiaremos una rama de las matemáticas que aborda problemas en los que intervienen elementos de ambas disciplinas. En esta rama, conocida como geometría analítica, se introduce el empleo de sistemas de coordenadas, mediante los cuales se pueden aplicar procedimientos algebraicos para estudiar situaciones geométricas y viceversa.
La geometría analítica estudia los elementos de la geometría euclidiana refiriéndolos a sistemas de coordenadas, como el cartesiano. En este texto nos limitaremos a estudiar solamente algunas figuras respecto de dicho sistema coordenado. Por lo tanto:
El propósito de la asignatura es que el estudiante interprete, argumente, comunique y resuelva diversas situaciones
problemáticas de su contexto por medios gráficos y analíticos, que incluyan la representación de figuras en el plano cartesiano.
Estructura de la asignatura
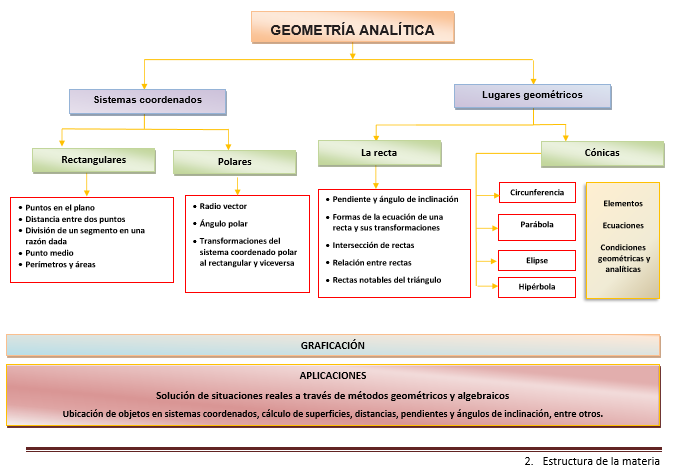
Introducción a la geometría analítica
La historia del origen de la Geometría es muy similar a la de la Aritmética, siendo sus conceptos más antiguos consecuencia de las actividades prácticas. Los primeros hombres llegaron a formas geométricas a partir de la observación de la naturaleza.
Durante el siglo XVII surgieron casi todas las disciplinas matemáticas, produciéndose en lo que a la geometría se refiere el nacimiento de la geometría analítica. Sin duda los dos grandes en esta materia y época fueron René Descartes (1596-1650) y Pierre de Fermat (1601-1655).
Las ideas de la geometría analítica, es la introducción de coordenadas rectangulares y la aplicación a la geometría de los métodos algebraicos, esto se concentra en una pequeña obra: "Introducción a la teoría de los lugares planos y espaciales". Aquellos lugares geométricos representados por rectas o circunferencias se denominaban planos y los representados por cónicas, espaciales.
Fermat abordó la tarea de reconstruir los "Lugares Planos" de Apolonio, describiendo alrededor de 1636, el principio fundamental de la geometría analítica: "siempre que en una ecuación final aparezcan dos incógnitas, tenemos un lugar geométrico, al describir el extremo de uno de ellos una línea, recta o curva".
Lo que sí está totalmente demostrado, es que la introducción del método de coordenadas deba atribuirse a Fermat y no a Descartes, sin embargo su obra no ejerció tanta influencia como la Geometría de Descartes, debido a la tardanza de su edición y al complejo lenguaje algebraico utilizado
El desarrollo posterior de la geometría analítica, mostró que las ideas de Descartes sobre la unificación del álgebra y geometría no pudieron realizarse sino que siguieron un camino separado aunque relacionado.
El surgimiento de la geometría analítica, aligeró sustancialmente la formación del análisis infinitesimal y se convirtió en un elemento imprescindible para la construcción de la mecánica de Newton, Lagrange y Euler, significando la aparición de las posibilidades para la creación del análisis de variables.
La historia de las matemáticas considera a René Descartes el fundador del sistema matemático moderno y por lo tanto el padre de la geometría analítica.
El cálculo y la geometría analítica marcan el comienzo de las matemáticas modernas en el siglo XVII.
Para que te des cuenta de la importancia que tiene la historia, te invito a que describas algunas aportaciones a la Geometría Analítica de René Descartes y Pierre Fermat en el formato siguiente, desarrollando la nota respectiva en tu cuaderno de notas.
|
Científico
|
René Descartes |
Pierre Fermat |
|
Aportación
|
__________________________________
__________________________________ |
__________________________________
__________________________________ |
Competencias por desarrollar:
Genéricas:
- 5.1 Sigue instrucciones y procedimientos de manera reflexiva, comprendiendo como cada uno de sus pasos contribuye al alcance de un objetivo.
- 5.6 Utiliza las tecnologías de la información y comunicación para procesar e interpretar información.
-
6.4 Estructura ideas y argumentos de manera clara, coherente y sintética.
- 8.3 Asume una actitud constructiva, congruente con los conocimientos y habilidades con los que cuenta dentro de distintos equipos de trabajo.
9. Participa con una conciencia cívica y ética en la vida de su comunidad, región, México y el mundo.
9.3 Conoce sus derechos y obligaciones como mexicano y miembro de distintas comunidades e instituciones, y reconoce el valor de la participación como herramienta para ejercerlos.
Disciplinares
1. Construye e interpreta modelos matemáticos mediante la aplicación de procedimientos aritméticos, geométricos y variacionales, para la comprensión y análisis de situaciones reales, hipotéticas o formales.
2. Formula y resuelve problemas matemáticos, aplicando diferentes enfoques.